Case Study:
Fuel economy of the SD40 locomotive
One of my favorite personal web sites to browse (now sadly offline — links are via the Wayback Machine) was BNSF engineer Al Krug’s “Tales from the Krug”, a collection of illustrated stories about his experiences working on the former CB&Q between Sheridan, Wyoming, and Billings, Montana. His Railroad Facts and Figures page had the best layman’s descriptions of how railroad signals work, and how much horsepower is needed to move a train up a grade, that I have ever seen.

One of his Facts and Figures pages discussed the fuel efficiency of various locomotives. Locomotives don’t have a continuously variable “gas pedal” like cars and trucks do. They have a throttle which can be placed in one of eight notches (power settings). Engines don’t run equally efficiently at all speeds and all loads. Mr. Krug reproduced this table describing the fuel efficiency of the EMD SD40. The SD40 and its successor the SD40-2 were built for more than 30 years, with more than 4,000 units sold — the single best-selling locomotive of all time, a common sight on the main line in my childhood, and still a common sight in shortline and switching service today.
EMD SD40 Fuel Efficiency
| Notch | Gal/Hour | Horsepower | Hp-Hr/Gal |
| 8 | 167.7 | 3000 | 17.9 |
| 7 | 145.8 | 2375 | 16.3 |
| 6 | 108.5 | 1830 | 16.9 |
| 5 | 79 | 1420 | 18.0 |
| 4 | 57.2 | 1085 | 19.0 |
| 3 | 41.4 | 710 | 17.1 |
| 2 | 24.9 | 390 | 15.7 |
| 1 | 7.4 | 200 | 27.0 |
| Idle | 5.5 | 0 | 0 |
The fuel efficiency differences are quite striking. This engine runs more efficiently in notch 4 than in notch 2 or 3; and more efficiently in notch 8 than in 6 or 7. If you need a certain horsepower, you use whatever notch gives you the power you need; but, if you had a choice, you would use notches 1, 4, 5, and 8, and avoid 2, 3, 6, and 7.
Our discrete optimization problem

Railroads very commonly use several locomotives to pull a train. A single crew controls all of the locomotives from the lead unit. Using 1940s-era electrical connections, the crew’s only option was to place the entire consist in the same notch. If you had 3 SD40s, and you needed 7000 HP, you selected notch 7, and (looking at the table above) you burned 437 gallons of fuel per hour to get 7125 HP.
But suppose, in this age of computerization and radio control, that we could set each unit to whichever notch we wanted. We could place two units in notch 8 and one unit in notch 4, and burn only 392 gallons per hour to produce our 7000 horsepower. The railroad would love to save $100 an hour in fuel costs. The environment would benefit from spewing a thousand pounds an hour less of CO2 into the atmosphere. The cost of installing the necessary radio receivers could be recouped in just a few months.
An engineer that had access to such a system would have a bewildering array of power settings to choose from. In the last days before SD40s were replaced by higher-horsepower modern units, railroads operated six or even eight of them together (see the photo at right). With six units, some three thousand different power settings are possible. Even with just three units, there are 164 different possibilities.
Our hypothetical engineer might like some advice from his mathematician friend. He might ask—
- For any desired HP output, what combination gets me closest to that exact power output?
- What are the recommended (most efficient) power settings?
- What is an efficient sequence of power settings such that we never reduce power on one unit while increasing total power?
Finding answers
It’s easy for a computer to make a list of all possible power settings, and select those that meet some set of criteria. For this essay we’ll confine ourselves to 3-unit consists.
For the first question, all we need is a list of settings sorted by horsepower. If you need at least 5200 HP, you look on the list, and you see the closest you can get is 7+5+5, generating 5215 HP and burning 303.8 GPH:
| Notches | Total HP | Total Gal/hr | ||
| 1 | 0 | 0 | 200 | 16.0 |
| 2 | 0 | 0 | 390 | 33.5 |
| 1 | 1 | 0 | 400 | 19.1 |
| … | ||||
| 8 | 5 | 3 | 5130 | 288.1 |
| 7 | 7 | 2 | 5140 | 316.5 |
| 8 | 4 | 4 | 5170 | 282.1 |
| 7 | 5 | 5 | 5215 | 303.8 |
| 8 | 6 | 2 | 5220 | 301.1 |
| … | ||||
| 8 | 8 | 5 | 7420 | 414.4 |
| 8 | 7 | 7 | 7750 | 459.3 |
| 8 | 8 | 6 | 7830 | 443.9 |
| 8 | 8 | 7 | 8375 | 481.2 |
| 8 | 8 | 8 | 9000 | 503.1 |
To answer the 2nd question, we have to be very precise in how we define our criteria.
Does “most efficient” mean “generating at least as much power than any other setting that burns less fuel than this one”? Is that the same thing as “burning less fuel than any power setting that produces more horsepower than this one”? (Yes. Fifty-six of the 164 possibilities satisfy this criterion.)
If we adopt that definition of “efficient” we would give our engineer a list of those 56 power settings to choose from. A partial list looks like this:
| Notches | Total HP | Total Gal/hr | ||
| 1 | 0 | 0 | 200 | 16.0 |
| 1 | 1 | 0 | 400 | 19.1 |
| 1 | 1 | 1 | 600 | 22.2 |
| 2 | 1 | 1 | 790 | 39.7 |
| 3 | 1 | 0 | 910 | 53.1 |
| … | ||||
| 7 | 5 | 4 | 4880 | 282.0 |
| 8 | 4 | 4 | 5170 | 282.1 |
| 8 | 6 | 2 | 5220 | 301.1 |
| 8 | 5 | 4 | 5505 | 303.9 |
| … | ||||
| 8 | 8 | 5 | 7420 | 414.4 |
| 8 | 8 | 6 | 7830 | 443.9 |
| 8 | 8 | 7 | 8375 | 481.2 |
| 8 | 8 | 8 | 9000 | 503.1 |
Note that the very inefficient 7+5+5 setting we found in our first list has been deleted. In fact only six of the 56 entries on this list, vs. 45 of the original 164 power settings, has even one unit in notch 7, and none ever has two units in notch 7.
That isn’t the only possible definition of “efficiency.” You might, for instance, notice that the best fuel economy possible is with all 3 units in notch 1 (600HP on 22.2 GPH, for 27.03 hp-hr/gal), and ask for a list of settings such that no higher-horsepower setting achieves better fuel economy. Only thirteen of the 164 power settings merit inclusion on this list:
| Notches | Total HP | Total Gal/hr | |||
| 1 | 1 | 1 | 600 | 22.2 | 27.03 |
| 4 | 1 | 1 | 1485 | 72.0 | 20.63 |
| 4 | 4 | 1 | 2370 | 121.8 | 19.46 |
| 4 | 4 | 4 | 3255 | 171.6 | 18.97 |
| 8 | 1 | 1 | 3400 | 182.5 | 18.63 |
| 5 | 4 | 4 | 3590 | 193.4 | 18.56 |
| 8 | 4 | 1 | 4285 | 232.3 | 18.45 |
| 8 | 4 | 4 | 5170 | 282.1 | 18.33 |
| 8 | 5 | 4 | 5505 | 303.9 | 18.11 |
| 8 | 8 | 1 | 6200 | 342.8 | 18.09 |
| 8 | 8 | 4 | 7085 | 392.6 | 18.05 |
| 8 | 8 | 5 | 7420 | 414.4 | 17.91 |
| 8 | 8 | 8 | 9000 | 503.1 | 17.89 |
Using just these 13 power settings would both give the engineer more flexibility than the original eight, and produce substantially better fuel economy.
Question 3 raises a practical problem with using those power settings, however. When, 1940s style,we open the throttle successively from notch 1 to notch 8, all three units rev up steadily until reaching maximum power. If we “increased power gradually” according to the table above, individual units would cycle repeatedly from low to high power unnecessarily. As a practical matter, it would be much easier on the equipment — and provide smoother acceleration — to progress directly from 4+4+4 to 5+4+4, not from 4+4+4 to 8+1+1 and then back to 5+4+4.
We could simply strike 8+1+1, 8+4+1, and 8+8+1 from our list of recommended power settings, so that every change from A+B+C to X+Y+Z had A<=X, B<=Y, and C<=Z. Or we could formulate a new optimization task with a new criterion. For instance: Choose a sequence of 25 steps, 0+0+0, 1+0+0, … 8+8+7, 8+8+8, each step increasing power on one unit by one notch, such that we favor efficient combinations whenever possible.
Then we have to choose a way of measuring efficiency. We could just ask which set of 25 steps includes as many as possible of the 56 steps we identified in Question 2A. Or we could choose some more complicated criterion that took into account how inefficient each non-ideal step was.
This is a much harder discrete optimization problem than any previously considered in this essay. There are 23,371,634 possible sequences to consider! (With k units each with n throttle notches, the number of sequences is given by the nth k-dimensional Catalan number.)
Solving this problem by brute-force search is feasible, on a fast modern computer with an efficiently written program. (And I did enumerate all 23 million sequences, to find all the candidates.) But if the problem were any larger — 4 units rather than 3, say — brute force becomes too slow, and we must “work smart, not hard.”
We know that the bottom end of the sequence is surely 100 110 111 211 311 411, and the top end is surely 885 886 887 888. We know that 5+5+5 is worse than 8+4+1. The only questions we have are whether the best path is going to be 411 > 441 > 841 > 844 > 884, or 411 > 441 > 444 > 844 > 884, or a handful of others. In effect, 0 1 4 5 and 8 are the only notches we care about, and it’s easy to solve this much smaller problem by hand.
There are eight sequences where every step from 000 to 888 is included in the list of 56 most efficient steps. They differ only in how much they use notch 5. All of these sequences begin 000 100 110 111 211 311 411 421 431 441 442 443 444, all of them pass through 854, and all of them end 885 886 887 888. But you have a choice between 444 544 644 654 754 854 or 444 544 554 654 754 854 (when to move the second unit to notch 5); and you have a choice between 854 864 874 884 885, 854 864 874 875 885, 854 864 865 875 885, and 854 855 865 875 885 (when to move the third unit to notch 5.)
We can prove those are the only eight sequences, by noting that 744 is not on the list of most efficient throttle positions (so we can’t go from 444 to 844). Similarly we can rule out going from 441 to 841 becuase 641 is not on the list; and from 841 to 881, because 861 is not on the list.
So how much fuel would this have saved?
This new system would save fuel in two ways. One, it would avoid very inefficient configurations like 666 and 777. Two, more virtual “notches” make it possible to more closely match the desired power, and make fewer power setting changes. On the graph above, notice that the “old” and “new” settings coincide, from 400-600, 2880-3255, and 8375-9000 HP, where both methods have all units in notch 1, notch 4, and notch 8, respectively. Everywhere else, the new power settings provide substantially greater fuel efficiency.
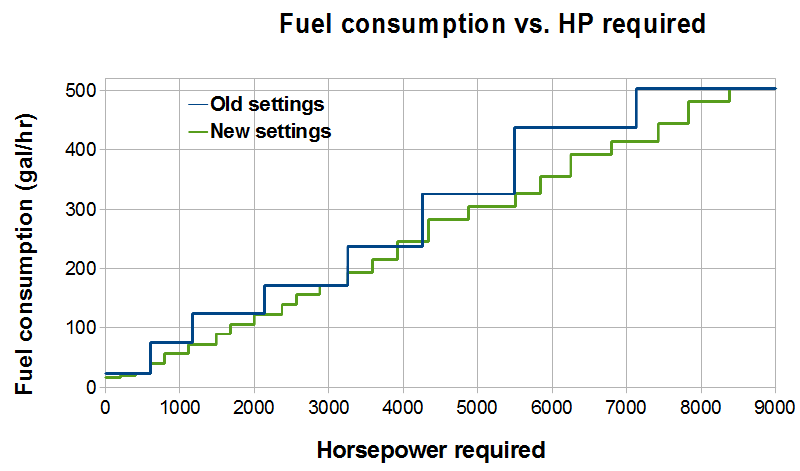
Calculating the exact savings at any given power setting requires a bit of additional math.
If a train requires, say, 6000 HP to maintain the desired speed, traditionally an engineer has to move back and forth between notch 6 and notch 7: he would spend about 31% of the time in notch 7 (7125HP) and 69% in notch 6 (5490 HP), for an average fuel consumption of about (.31)(437)+(.69)(325)=360 gallons per hour.
Using this hypothetical new set of power settings, to produce an average of 6000 HP, the engineer would spend 60% of his time in 8+6+5 (6250HP) and 40% in 8+5+5 (5840HP), resulting in smoother train handling, and an average fuel consumption of about (.60)(355)+(.40)(326)=344 gallons per hour.
So why don’t real railroads do this?
Presumably, the need for doing so is less pressing today than it was 40 years ago when SD40s were in common use. If newer locomotives don’t suffer as much of an efficiency penalty in notch 6, there is no need to go to a lot of trouble to operate in 8+5+4 instead of 6+6+6.
I am told that some railroads did in fact have a primitive version of this mechanism, which allowed the engineer to choose to take units offline. This doesn’t allow the full range of possibilities, but does allow for two units to be run in the same notch while the third is at idle.
In the 21st century it is common to have ‘distributed power’, engines on both head end and rear of a freight train, and the capacity exists to control each block of units separately.
Back to Discrete Optimization page
Back to main optimization page
