Discrete Optimization

Do you have an optimization problem you need help with? Contact us for a free consultation and estimate.

Discrete optimization problems are those where a finite set of alternatives need to be considered, and calculus-based methods of finding maxima and minima don’t apply.

Improving the fuel economy of SD40s (full size version in linked article)

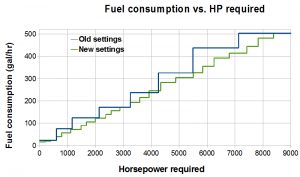
For an in-depth example of discrete optimization, see our analysis of most efficient throttle positions on diesel locomotives: unlike a car or truck driver who can smoothly vary the position of the gas pedal, a train engineer can only choose one of eight power settings. Traditionally, when a train is pulled by more than one locomotive, all units use the same power setting. But it may be possible to improve the train’s fuel economy by 5 to 10%, if you have a way to control each locomotive separately.

There may or may not be a random component in how each alternative is evaluated. The railroad example above includes no randomness at all. Similarly, when Google Maps shows you the shortest route between your house and mine, there is no randomness, just a decision to be made at each road junction along the way. (If you ask Google for the fastest route, now there is a random component: it must estimate how much time you will spend stuck at red lights or in slow-moving traffic.)

What’s your best chance to make 4H?

Pictured at right is a a simple card-combination problem you may face if you play contract bridge.
There is no randomness in your own actions, but there is uncertainty about what cards our opponents were dealt, and there is more than one way we might face that uncertainty.

Holding K-J-3-2 opposite A-9-6-4, you face a series of discrete choices: Do you want North or South to lead? If south, do you lead the ace, the nine, or a small card? If West plays the five on your four, do you play the king, the jack, or a small card from North? And then, next time you lead hearts, which of the three remaining cards will you lead?

If your goal is to maximize the expected number of tricks you will win, the right play is small from south and the jack from north on the first trick, then cashing the ace and king on the second and third tricks. You will win 3.34 tricks, on average, in this suit. If you need to win four tricks, the right play is the same. You will succeed 37% of the time (any time your opponent’s cards are divided 3-2, and West holds the queen.) But if your goal is to guarantee winning at least three tricks, you do so by leading small from south, playing the king from North, then leading small from North intending to play the nine from South. This amounts to buying insurance: we are reducing our expected number of winners from 3.34 to 3.20, in exchange for a 100% chance of three tricks instead of only a 97% chance.

If you are playing Four Hearts (contracting to win 10 of the 13 tricks) on the cards pictured at right, playing the king to guarantee 10 tricks is the right action in a social bridge game (scored by total points) or a team game (scored by IMPs).