Resource Allocation

To get the most out of a limited research budget, collect just enough data to answer your questions, but no more. Ask us how we can help you decide how much is just enough.

Resource allocation is one of the most important practical applications of optimization techniques.

Researchers almost never have the luxury of collecting all the data we want. A bookstore owner can’t afford to keep one copy of every book in print on hand. A car dealership can’t afford to keep an example of every make, model, color, and options package on the lot; they stock the most popular models, and enough different options combinations so they can show customers what is available by special order. Fast food restaurants pre-cook the most popular items on their menu so that customers can get instant service — but they run the risk of having to throw out cold stale food if nobody orders a Whopper for an hour. How do you balance the benefit of faster service against the risk of waste?

Even in Alaska, moose order dinner from drive-through windows rarely, and keeping fresh willows on hand is not cost-effective for the restaurant. This photo has been making the rounds for at least a dozen years.

You create a mathematical model which idealizes your problem. In the case of the fast-food restaurant, we need to—

• Assign a dollar value to the cost of slow service: say, our average profit per drive-through customer is $10, and if we have a customer’s order pre-cooked, he will wait at the window for 2 minutes rather than 5. If we pre-cooked every item on the menu, we would make $300 an hour. Every time we make a lineup of customers wait, the 3-minute delay means we can do $15 less business. (If nobody is waiting in line, we don’t lose out on any business, but we do frustrate one customer. Maybe we assign this a cost of $1, by making that customer slightly less likely to come back.)
• Assign a dollar value to the cost of wasted food: say, it costs $2 to make a sandwich, and if it sits unsold for half an hour, we throw it away.
• Collect data about how much of the time the drive-through window is busy.
• Collect data about how often each item on the menu is purchased.

Then we can calculate whether the benefit of serving customers faster is worth the cost of potentially wasting food. Suppose that during the lunch rush, we sell 20 hamburgers per hour, but only 2 barbecue bison burgers per hour, and there is a line at the drive-through 80% of the time. It pays to pre-make both items. We could pre-cook several hamburgers, with almost no risk that they would go to waste. The pre-cooked bison burger will go to waste about 37% of the time (costing us $2), but if it sells, the time savings will be worth about $12. During the lunch rush, we should pre-cook menu items that sell as slow as 0.4 times per hour; even an 80% chance of the food going to waste may be acceptable, if it keeps the line moving faster.

Now suppose at 10:00 at night, we only sell 3 hamburgers an hour, and a bison burger once an hour, and there is almost never a line at the drive-through window. Now the cost of throwing out food is still $2 per sandwich, but the benefit of fast service is only $1 per customer. It still pays to keep one hamburger pre-made at all times — there is only a 22% chance it will go to waste — but any item that sells more slowly than about 2.2 per hour should not be.

Statistical applications of resource allocation methods

We applied queueing theory to calculate the probability of sandwiches going to waste in the above example.

The most common resource allocation questions involve collecting data efficiently. A telephone or internet interview can be conducted anywhere in the country at the same cost; but conducting a face-to-face interview, or collecting a water or soil sample, incurs travel costs. Even if local variations are smaller than regional variations, it may be much cheaper to travel to 50 sites, and collect 10 samples from a small area, than it is to travel to 200 widely separated sites. Both pollsters and field scientists widely use this method, cluster sampling.

The state of the US presidential race in October 2016, according to fivethirtyeight.com: to predict (or influence) the outcome of the election, concentrate your resources on Ohio, North Carolina, and Florida.

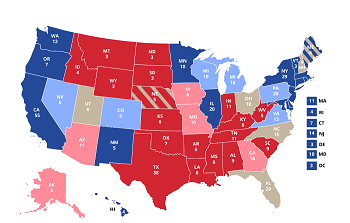
Another kind of allocation problem arises when your problem can be broken down into sub-problems, and you don’t need equally precise answers to each sub-problem. Suppose you are trying to predict the outcome of a presidential election. You may need to poll a thousand people to find out which candidate is ahead in a swing state like Ohio. But a very small sample confirms that the Republican is leading in Idaho and Texas. You do not care whether he’s ahead 60-40 or 70-30; you care only that he’s far enough ahead that the outcome of the election is not in doubt. You don’t waste time making a thousand phone calls in Idaho — or in California or Texas, even though they have large populations. If you have a budget for a fixed number of phone calls nationwide and want to maximize your confidence in your answer, a statistician can tell you how many calls to make in each state.

All but the simplest real-world experiments can be broken into sub-problems like this. Suppose you are collecting water samples and sending them to a lab to be analyzed. Is it better to do a cheap low-precision analysis on many samples, or to send a few samples for more expensive high-precision analysis? Suppose you want to know how many jellybeans are in a jar: should you concentrate your effort on measuring the volume of the jar very precisely, or on determining the average size and shape of the jellybeans? Contact us to help you design an experiment that has the most bang for your buck.

Deterministic applications of resource allocation

The same mathematics applies to allocation problems that don’t include a random component. These problems are also common in everyday life, and in business.

Suppose you want to improve your house’s insulation, you have a fixed amount of money to spend, and you want to know where you’ll get the best return on your investment. You can determine how much heat you are losing through a window, and look up the price and R-value of a new double- or triple-pane window; you can get a price quote for blowing foam insulation into void spaces in your walls; or you can buy rolls of fiberglass insulation at Home Depot and spread them out in your attic yourself — cheaper than hiring a contractor, but possibly only a small benefit if you already have a foot of fiberglass in your attic. You find the cost of each improvement, and the expected energy savings of each improvement, and choose to spend your money on the one with the best return on your investment.

On a larger scale, a railroad or a highway department can identify the worst bottlenecks in their system; calculate the cost of adding extra tracks or traffic lanes in those places; and decide where best to spend their limited budget for capacity improvements. Identifying those bottlenecks can involve a major network modeling effort or a field campaign to collect data. Contact us to help you create your sampling plan.

Some additional resource allocation problems are talked about on our discrete optimization and optimal strategies of games pages.